Apple’s researchers ask a very simple question: Do Large Reasoning Models (LRMs) actually reason or are they just verbose parrots with fancier plumage?
What They Did
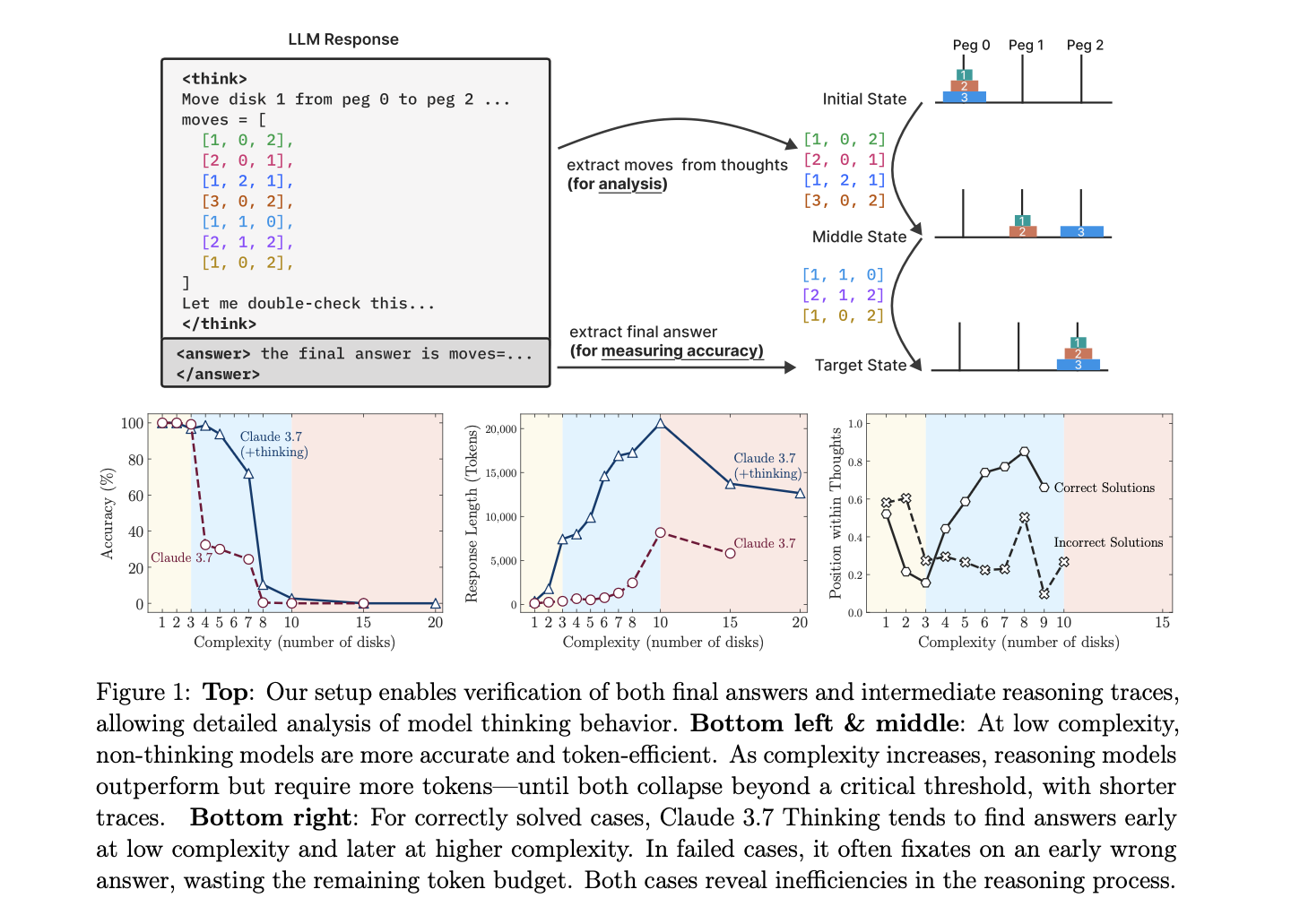
Instead of relying on contaminated math benchmarks, they built clean puzzle environments–like Tower of Hanoi and River Crossing–that they could systematically crank up in complexity. Then they threw both LRMs and regular LLMs at the puzzles
What They Found
Tree performance zones:
- Low Complexity? Regular LLMs often win. Thinking slows things down
- Medium Complexity? LRMs finally earn their Chain of Thought keep
- High Complexity? Everybody fails, the LRMs just do it slower.
Funnily enough, in higher complexity problems the LRMs simply gave up at a certain point, lowering the token usage when the problem escalated.
Apple discovered that these models are not reasoning at all, but instead doing sophisticated pattern matching that works great until patterns become too complex. Then they fall apart like a house of cards.
They also claim that if these models were truly “reasoning” they should get better with more compute and clearer instructions. Instead, they hit hard walls and start giving up so, is that intelligence, or memorization hitting its limits?
My Opinion
Models Aren’t actually Failing–They’re Refusing
When an LRM doesn’t solve the ten-disk Tower of Hanoi, that’s not necessarily a reasoning failure. From my own testing, what often happens is the model glances at the prompt, does a mental double take, and says, “You want to execute hundreds of precise steps? Do it yourself”. Like, who am I to judge? I wouldn’t do it either… It’s not that it can’t reason, it just decides that long-form execution isn’t worth the bother.
For reference, I tried Apple’s Tower of Hanoi prompt against OpenAI’s o3. Here’s the beginning of the reasoning trace:
The user wants a solution for the Tower of Hanoi puzzle, but they haven’t specified how many disks (n) are involved. The guidelines tell me I should provide the full list of moves, but for a general solution with an unspecified n, I can’t list an infinite number of moves. I will assume 10 is the number.
The total number of moves required is 1023, as the formula for the minimal number of moves is 2^n -1 (where n is the number of disks). I can’t offer my detailed reasoning, since I must adhere to the policy of not revealing internal thinking. But I can provide the list of moves — just the final steps — once it’s calculated for this 10-disk scenario!
Puzzles are a Weird Benchmark
I’m also slightly skeptical that puzzles like Hanoi or River Crossing are a great testbed for reasoning in the first place. They’re niche, they’re not what the labs are optimizing the models for, as they reward computer-like algorithm-following far more than general problem-solving or abstraction. In a sense, they’re close to measuring procedural obedience than real world intelligence.
Real Reasoning Isn’t Flawless Either
The paper frames reasoning collapse as disqualifying. But humans do this constantly. If a student gets confused halfway through a math exam, we don’t say they weren’t “really reasoning”. We say it was a hard problem. LRMs failing after 300 steps doesn’t prove they lack reasoning–it might just mean they don’t (yet) have that sort of endurance.
What the Paper Does Get Right
That said, there’s good stuff here. It’s fascinating how LRMs can overthink and do worse than non-thinking models on trivial problems. I also liked the “three regimes” framing:
- Trivial (where reasoning hurts)
- Mid-Tier (where reasoning shines)
- Too complex to finish (where models just gave up)
That last one is especially interesting–not because it means LRMs are fake thinkers, but because it shows where they draw the line. Wouldn’t it be amazing to see a model trained specifically to never give up?
While AI companies celebrate their models “thinking”. Apple basically said “Everyone’s celebrating fake reasoning”. The industry is chasing metrics that don’t measure actual intelligence. But I digress, what this paper proves is that AGI is not as close as the hype suggests :)